Cálculo Eléctrico

Hacemos una lista de algunas fórmulas de cálculo comunes que puede usar al elegir un relé de estado sólido (SSR) / módulo de estado sólido (SSM) o al diseñar un circuito.

Atención: HUIMU Industrial (HUIMULTD) no asume ninguna responsabilidad por errores en los datos ni en la operación segura y / o satisfactoria de los equipos diseñados a partir de esta información.

Fórmulas de cálculo de energía eléctrica

---

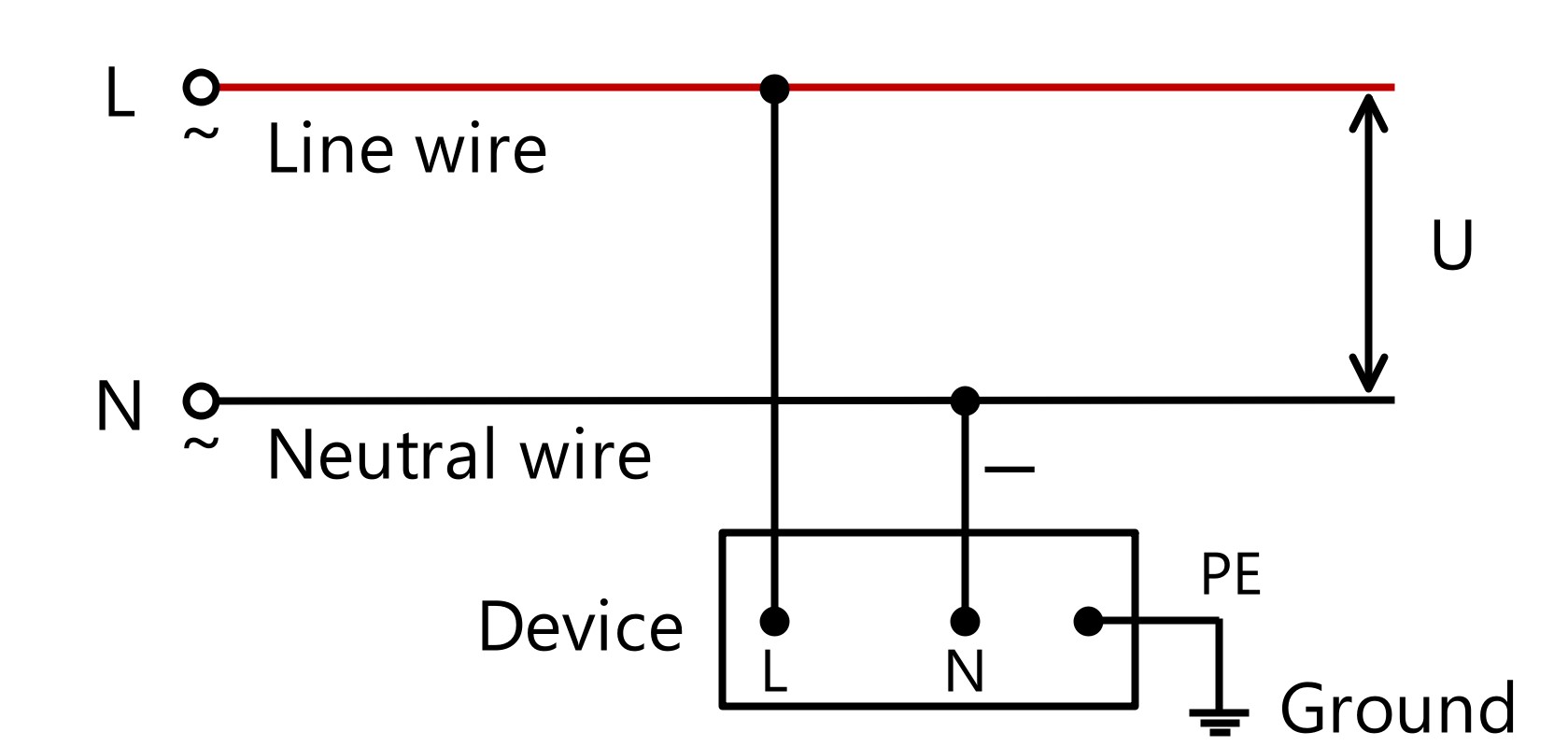
● Carga monofásica

P = U · I · cosφ
U es el voltaje (generalmente 220 VCA), I es la corriente.

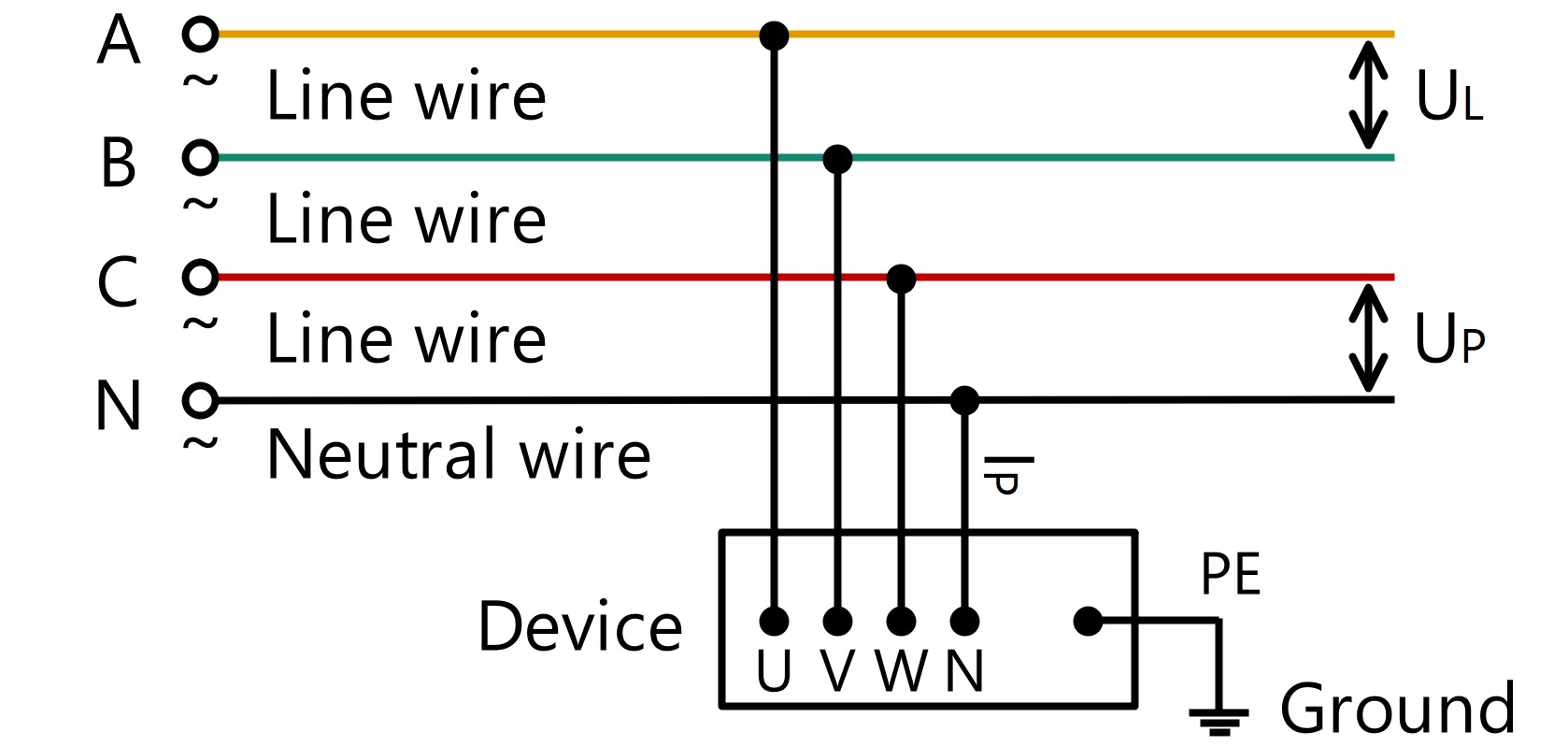
● Carga trifásica

P = √3 · U _L · I _L · cosφ = 3 · U _P · I _P · cosφ
U _L es el voltaje de línea (normalmente 380VAC), I _L es la corriente de línea, U _P es el voltaje de fase (normalmente 220VAC) , I _P es la corriente de fase.

● Factor de potencia (cos φ)

Si el tipo de carga es resistiva (como un calentador eléctrico), entonces cos φ = 1; Si el tipo de carga es inductiva (como un motor eléctrico), entonces 0 <cos φ <1. Tomemos como ejemplo el motor eléctrico, cuando el motor eléctrico está completamente cargado, la corriente activa es la más grande, la corriente reactiva es la más pequeña y el factor de potencia es de aproximadamente 0.85; cuando la carga es ligera o sin carga, la corriente activa es pequeña, la corriente reactiva es grande y el factor de potencia está entre 0.4 y 0.7. Por lo tanto, generalmente tomamos un factor de potencia de 0.78 o 0.8. Si el tipo de carga es la carga capacitiva (como el compensador de potencia), entonces cos φ <0.

● Valor pico, valor efectivo, valor promedio

El voltaje de CA es una onda sinusoidal, y su valor de voltaje cambia periódicamente de 0 al valor máximo (U _MAX ), por lo que su valor pico (U _PK ) es igual al valor máximo. El valor efectivo de CA se especifica por el efecto térmico de la corriente, es decir, deje que una corriente de CA y una corriente de CC pasen a través de resistencias con el mismo valor de resistencia respectivamente, y si generan el mismo calor al mismo tiempo, entonces el valor efectivo de esta corriente alterna es igual al valor de esta corriente continua. Dado que el valor efectivo del voltaje de CA sinusoidal es igual a su valor cuadrado medio raíz (U _RMS o U), U _RMSgeneralmente se usa para representar el valor efectivo del voltaje de CA. Normalmente, el valor de voltaje de CA que detectamos a través del equipo de detección (como multímetros) es el valor de voltaje efectivo, y el valor de voltaje de CA marcado en el equipo eléctrico también es el valor efectivo (como 220VAC, 380VAC). El voltaje de CA promedio (U _AV ) es el valor de voltaje promedio durante un período. El voltaje de CA promedio es igual a la integral del voltaje en un ciclo dividido por 2π (el tiempo en un ciclo). Teóricamente, el valor de voltaje de CC obtenido después de la rectificación de onda completa del voltaje de CA es igual al valor promedio del voltaje de CA.

U _PK = √2 · U _RMS = 1.414 · U _RMS
U _AV = 2 / π · U _PK = 0.637 · U _PK

De manera similar, de acuerdo con la ley de Ohm, podemos obtener el valor máximo (IPK o IMAX), el valor efectivo (IRMS) y el valor promedio (IAV) de la corriente alterna.

I _PK = √2 · I _RMS = 1.414 · I _RMS
I _AV = 2 / π · I _PK = 0.637 · I _PK

Debido a que el valor de corriente DC o voltaje DC es constante, no tienen valor máximo, valor efectivo y valor promedio.

Fórmulas de cálculo del factor de reducción

---

Dado que el rendimiento del módulo de estado sólido / relé de estado sólido se ve afectado por el entorno de trabajo y el tipo de carga, se debe considerar el Factor de reducción (o Factor múltiple actual) al seleccionar el valor de corriente nominal del módulo de estado sólido / relé de estado sólido .

I _R = I _L / α
I _R es el valor de corriente nominal del relé de estado sólido / módulo de estado sólido;
I _L es el valor de corriente de carga de CC o el valor efectivo de corriente de carga de CA (valor eficaz);
α es el factor de reducción.

Según el entorno de trabajo del módulo de relé de estado sólido / estado sólido (ventilación, temperatura, tiempo de servicio, etc.), el factor de reducción se puede dividir en tres niveles: Protegido, Normal y Severo.
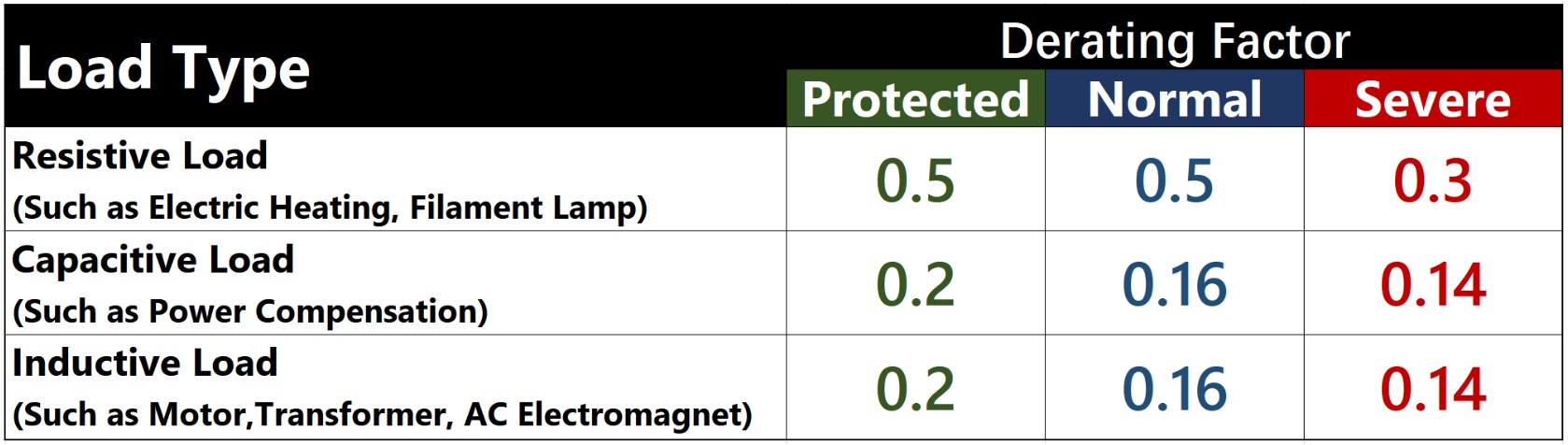
Para cargas resistivas (como calentador eléctrico, lámpara incandescente, etc.), α = 0.5 (Protegido), α = 0.5 (Normal), α = 0.3 (Grave);
Para cargas inductivas (como motor, transformador, etc.), α = 0.2 (Protegido), α = 0.16 (Normal), α = 0.14 (Severo);
Para cargas capacitivas (como compensador de potencia, etc.), α = 0.2 (protegido), α = 0.16 (normal), α = 0.14 (grave).

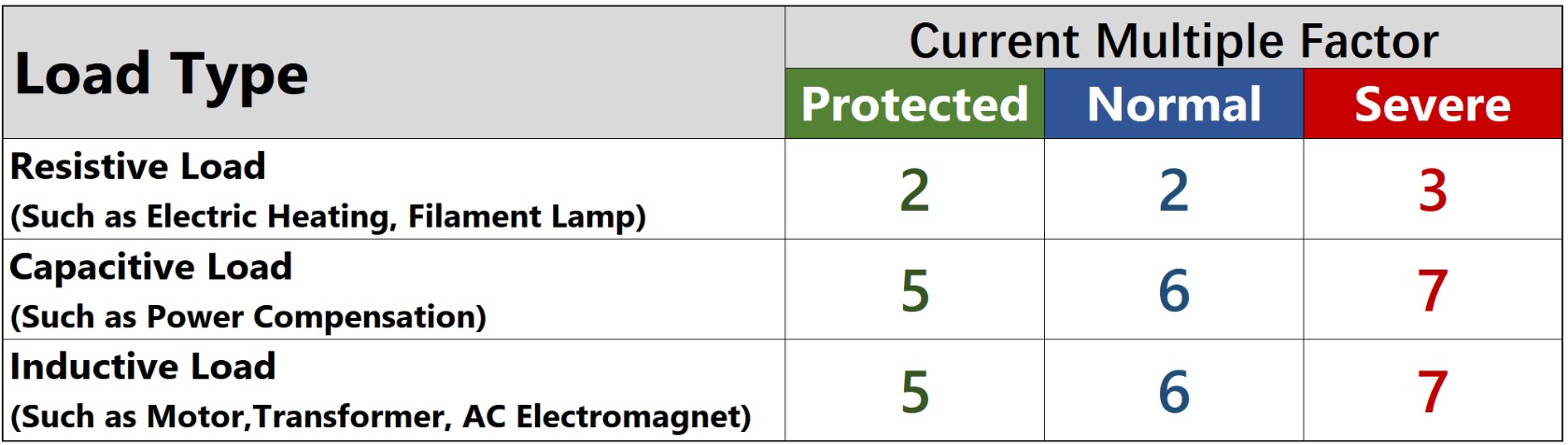
El Factor Múltiple Actual es el inverso del Factor de Reducción.

I _R = I _L · β
I _R es el valor de corriente nominal del relé de estado sólido / módulo de estado sólido;
I _L es el valor de corriente de carga de CC o el valor efectivo de corriente de carga de CA (valor eficaz);
β es el factor múltiple actual.

Para cargas resistivas (como calentadores eléctricos, lámparas incandescentes, etc.), β = 2 (protegido), β = 2 (normal), β = 3 (grave);
Para cargas inductivas (como motor, transformador, etc.), β = 5 (protegido), β = 6 (normal), β = 7 (grave);
Para cargas capacitivas (como compensador de potencia, etc.), β = 5 (protegido), β = 6 (normal), β = 7 (grave).

Por ejemplo, si necesita un relé de estado sólido del panel de CC a CA para cambiar una carga resistiva de 220 VCA y 10 A, y requiere que este relé de estado sólido funcione ininterrumpidamente en un entorno de ventilación deficiente, entonces de acuerdo con el factor de reducción β = 3 (Severo), debe elegir MGR-1D4830 (DC a AC, carga: 480VAC, 30A).

Fórmulas de cálculo de varistor

---

Si el voltaje pico de carga es alto, asegúrese de conectar el varistor (como MOV, ZNR) en paralelo al terminal de salida del relé de estado sólido / módulo de estado sólido.

V _imA = V _1mA = (a · v) / (b · c)
V _imA es el voltaje del varistor cuando la corriente es XmA. Debido a que el valor actual generalmente se establece en 1 mA, también se puede expresar como V 1 _mA ; a es el coeficiente de fluctuación de voltaje, generalmente 1.2; b es el valor de error del varistor, generalmente 0,85; c es el coeficiente de envejecimiento del componente, generalmente 0.9; v es el voltaje de funcionamiento de CC o el voltaje de CA rms.

Por lo tanto, la fórmula anterior se puede simplificar como:
Para circuito de CC, V _imA ≈1.6 · v
Para circuito de CA, V _imA ≈1.6 · V _p = 1.6 · √2 · V _AC
V _p es el voltaje máximo, V _AC es el valor efectivo

Generalmente, el voltaje del varistor es 1.6 veces el voltaje de la carga, pero cuando la carga es una carga inductiva, el voltaje del varistor debe ser 1.6-1.9 veces el voltaje de la carga para garantizar la seguridad.

Fórmulas de cálculo del circuito rectificador

---

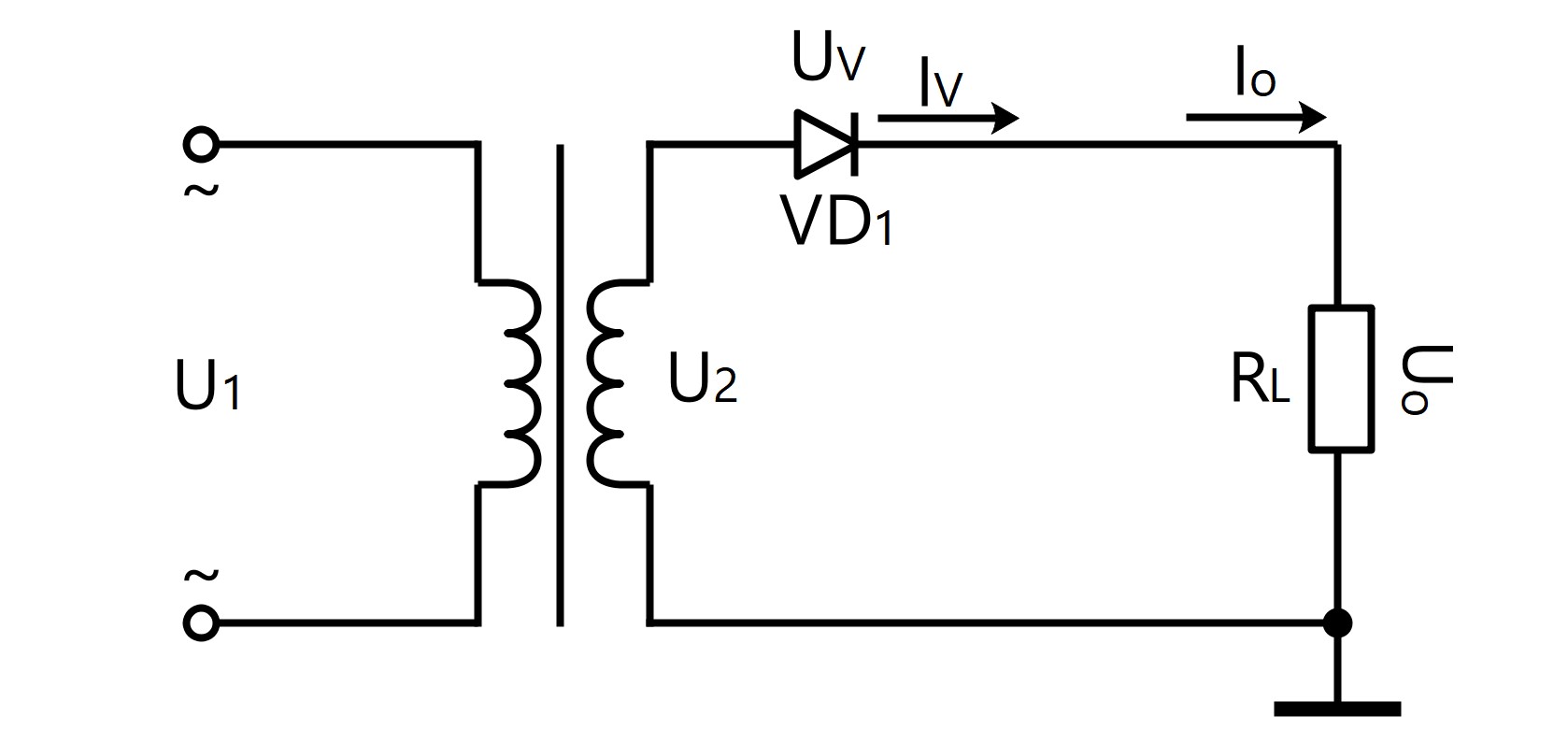
● Circuito de rectificación de media onda monofásico

U ₀ = 0.45 · U ₂
I ₀ = 0.45 · U ₂ / R _L
I _V = I ₀
U _RM = √2 · U ₂

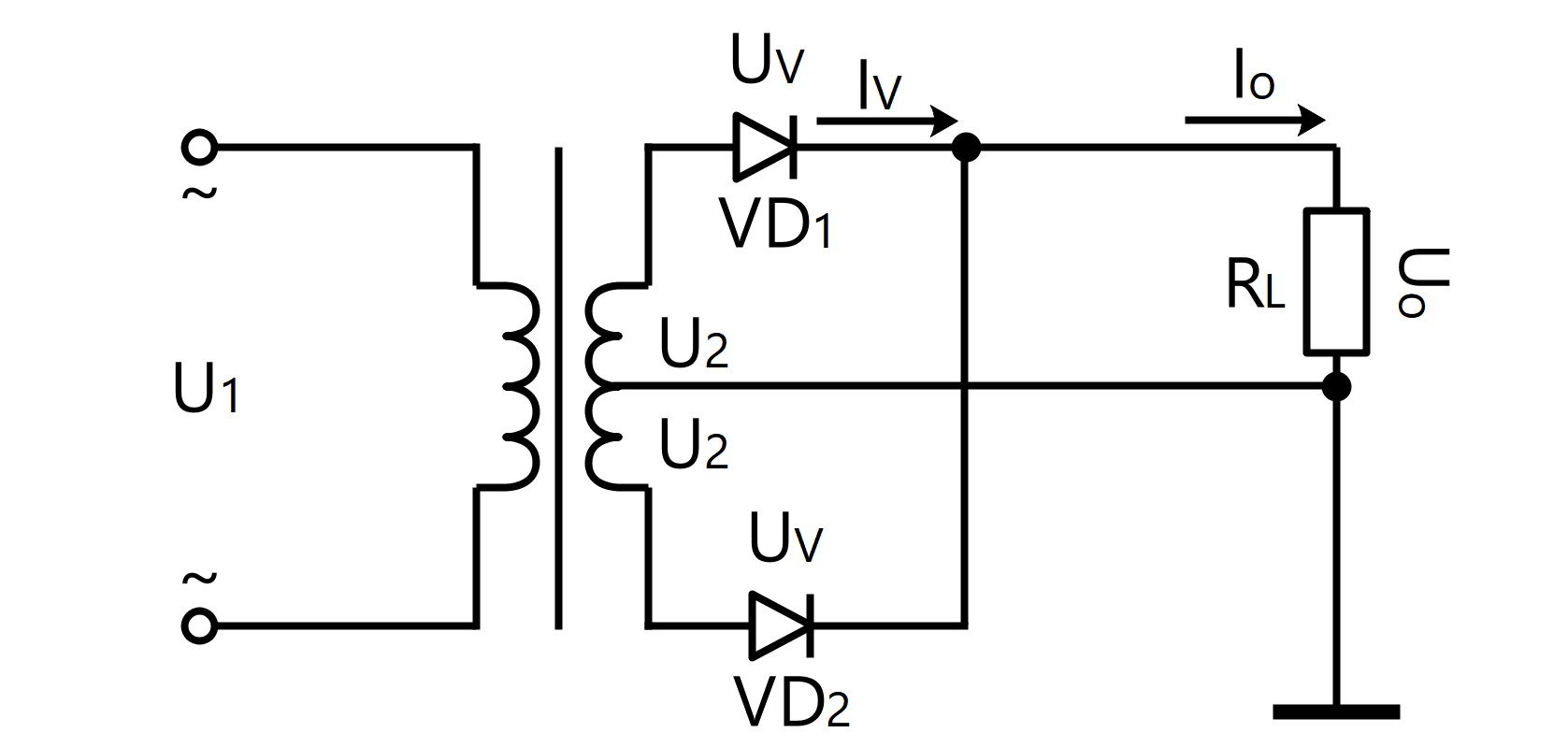
● Circuito de rectificación de onda completa monofásico

U ₀ = 0.9 · U ₂
I ₀ = 0.9 · U ₂ / R _L
I _V = 1/2 · I ₀
U _RM = 2 · √2 · U ₂

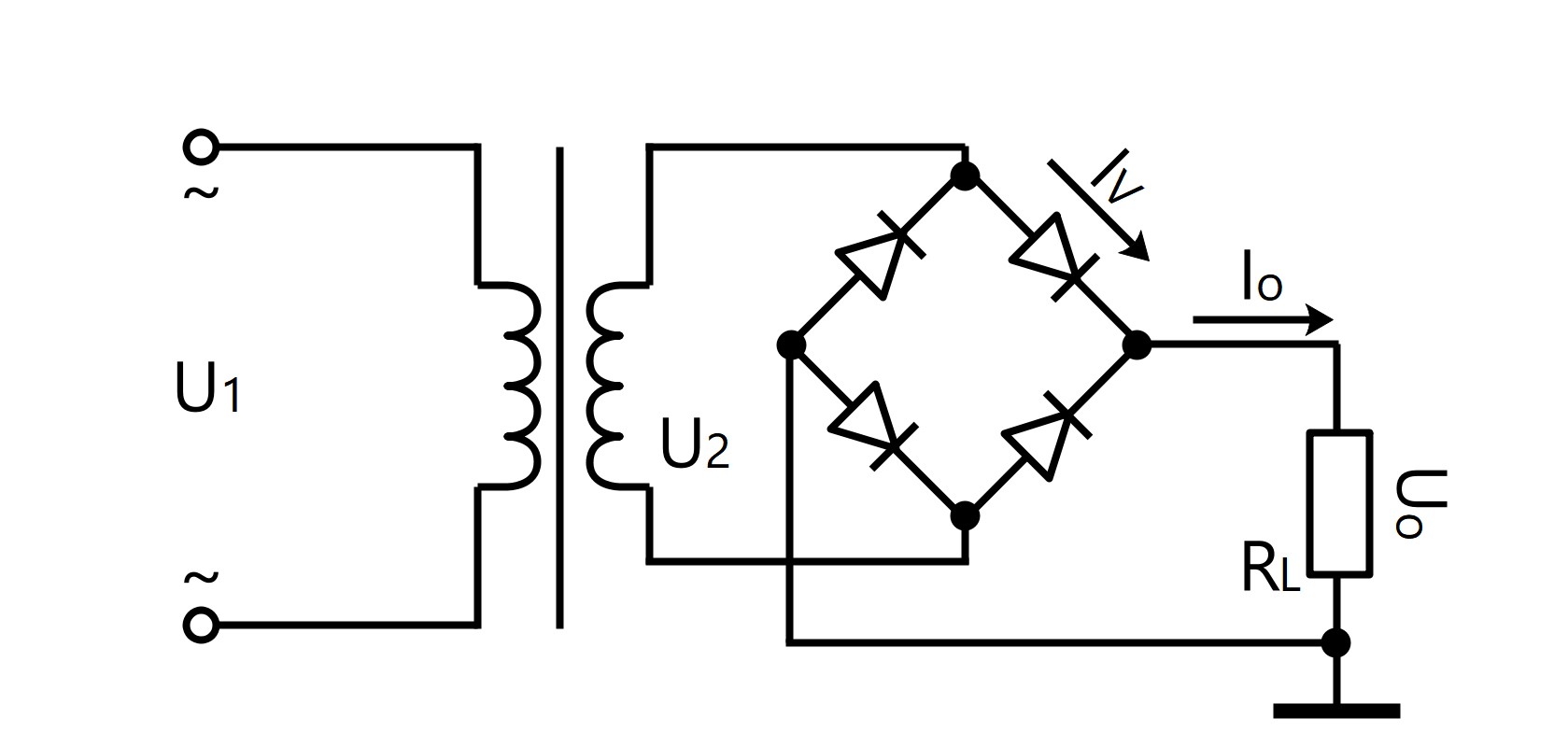
● Circuito de rectificación de puente monofásico

U ₀ = 0.9 · U ₂
I ₀ = 0.9 · U ₂ / R _L
I _V = 1/2 · I ₀
U _RM = √2 · U ₂

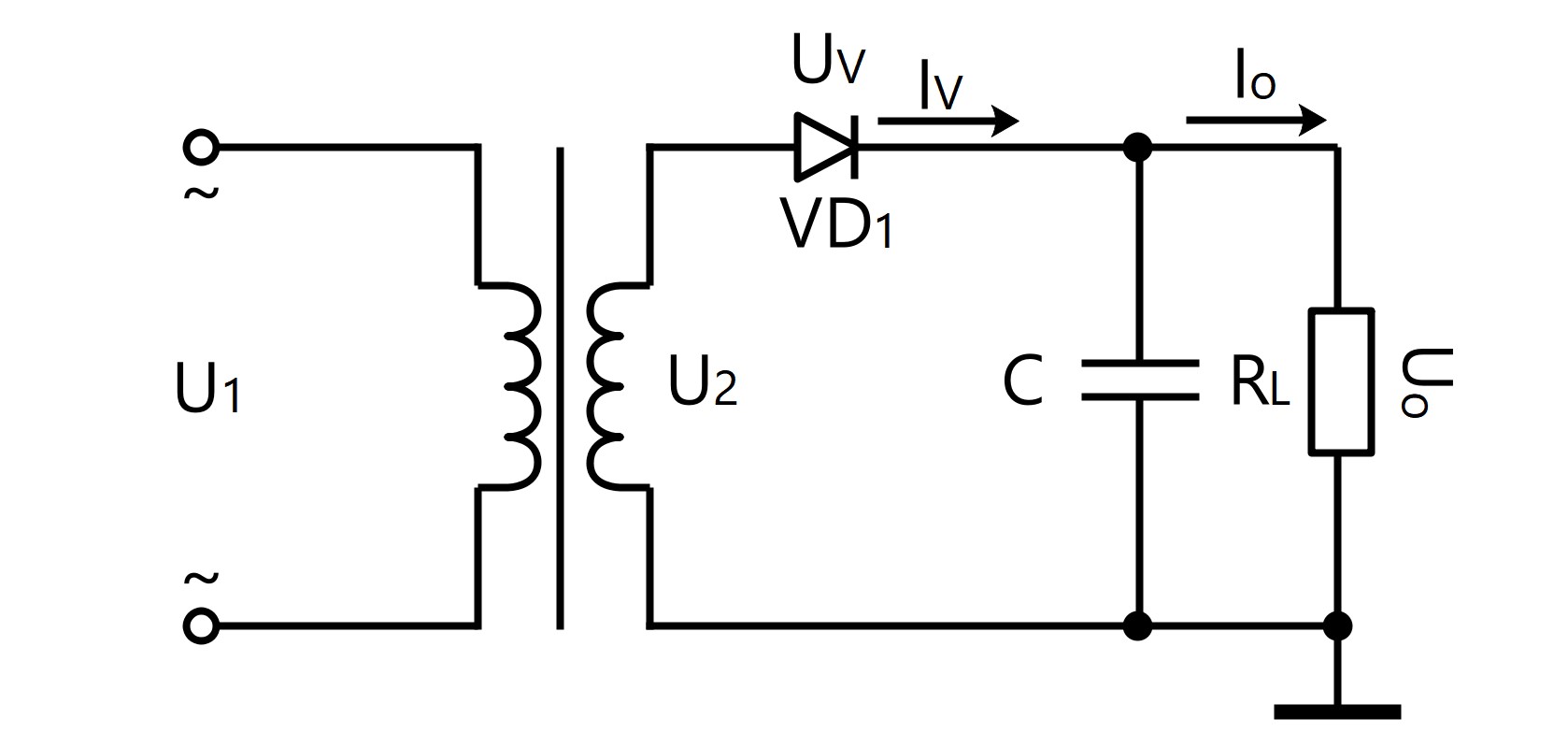
● Circuito de filtro de rectificación de media onda monofásico

U ₀ = U ₂
I ₀ = U ₂ / R _L
I _v = 1/2 · I ₀
U _RM = 2 · √2 · U ₂
C≥ (3 ~ 5) · T / R _L
T = 1 / f, si f = 50Hz, entonces T = 1/50 = 20ms

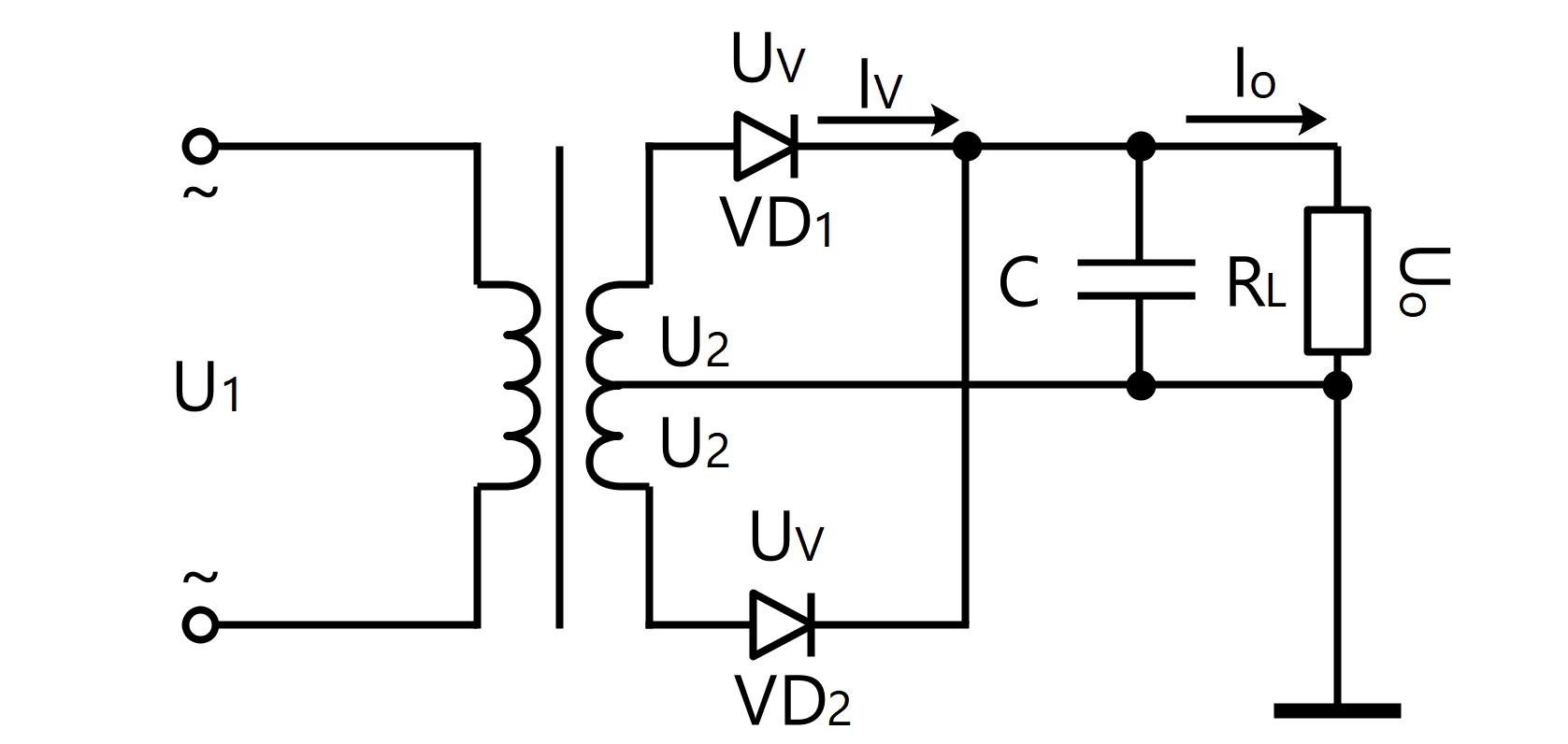
● Circuito de filtro de rectificación de onda completa monofásico

U ₀ = 1.2 · U ₂
I ₀ = 1.2 · U ₂ / R _L
I _v = 1/2 · I ₀
U _RM = √2 · U ₂
C≥ (3 ~ 5) · T / 2R _L
T = 1 / f, si f = 50Hz, entonces T = 1/50 = 20ms

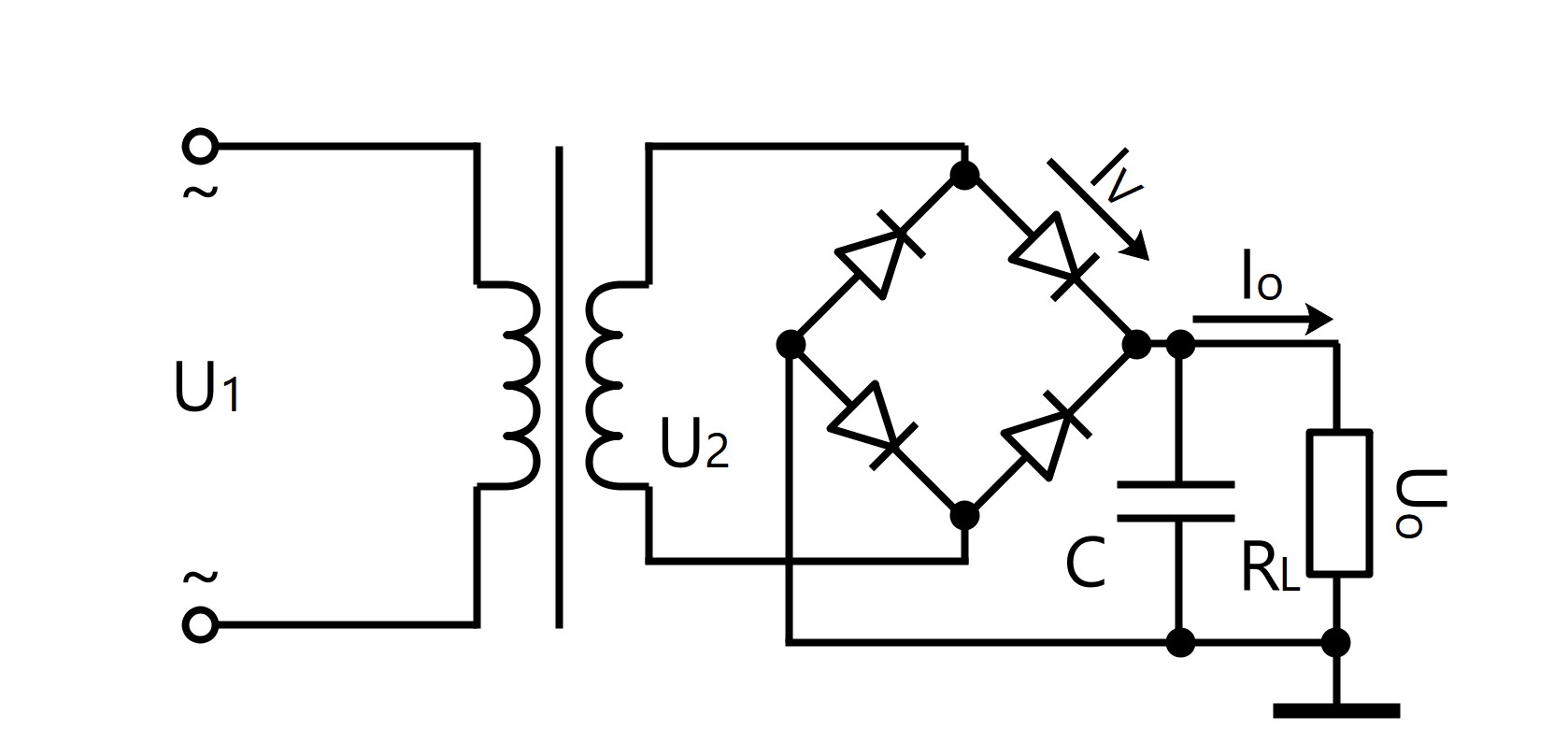
● Circuito de filtro de rectificación de puente monofásico

U ₀ = 1.2 · U ₂
I ₀ = 1.2 · U ₂ / R _L
I _v = 1/2 · I ₀
U _RM = √2 · U ₂
C≥ (3 ~ 5) · T / 2R _L
T = 1 / f, si f = 50Hz, entonces T = 1/50 = 20ms

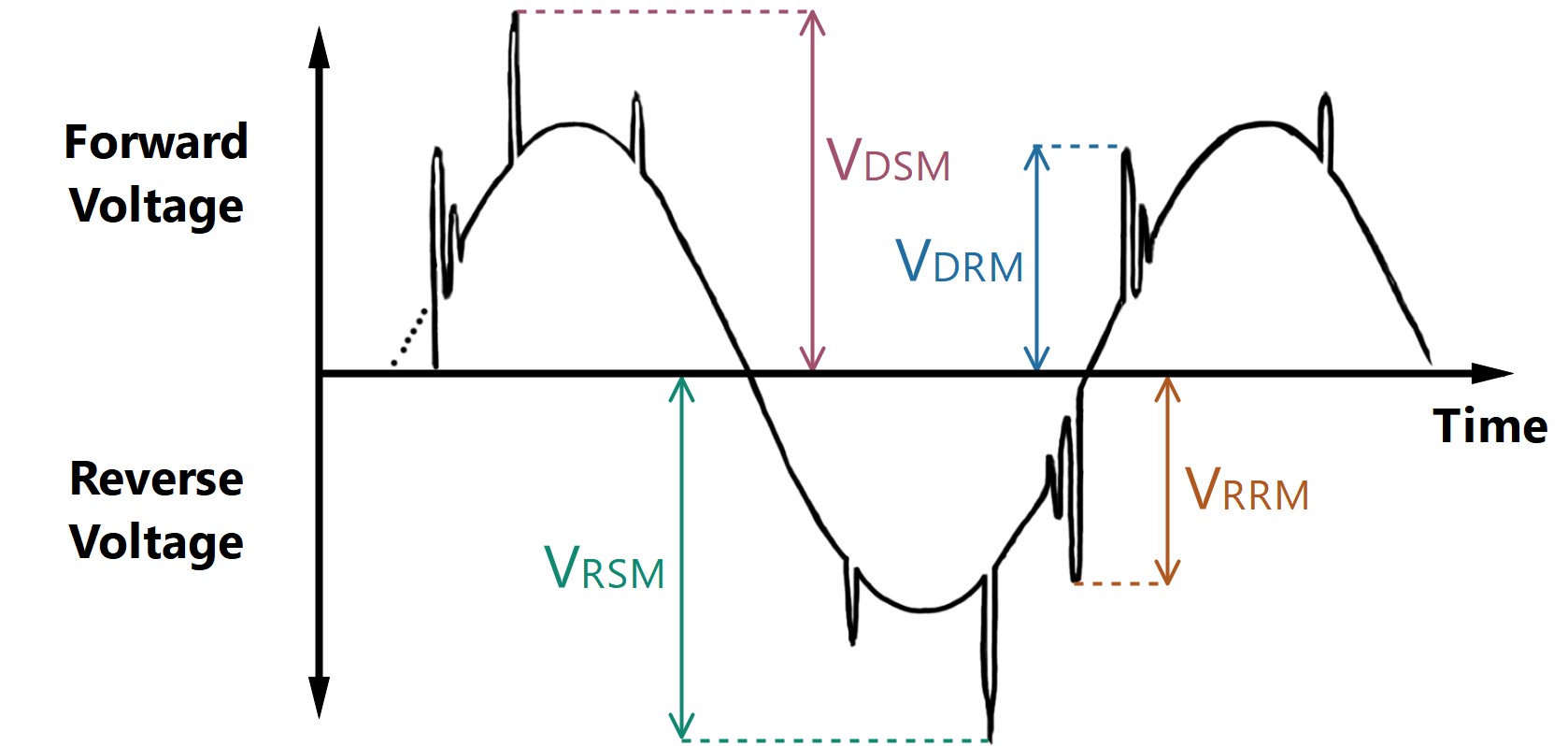
V _RSM = V _RRM + 200V
V _RSM (Voltaje inverso de pico no repetitivo), es el valor de sobrevoltaje máximo permitido de voltaje inverso que se puede aplicar a la dirección inversa del dispositivo; V _RRM (Voltaje inverso de pico repetitivo), es el valor máximo permitido de voltaje inverso que puede aplicarse repetidamente a la dirección inversa del dispositivo.

V _DSM = V _DRM + 200V
V _DSM (Voltaje de estado apagado máximo no repetitivo), es el valor máximo admisible de sobretensión del voltaje en estado apagado que se puede aplicar a la dirección directa del dispositivo; V _DRM (Voltaje repetitivo pico en estado apagado), es el valor máximo permitido de voltaje en estado apagado que se puede aplicar repetidamente a la dirección de avance del dispositivo.

I _t ² = I _TSM ² · t _w / 2
t _w es el período de medio seno; I _TSM es la corriente de sobretensión máxima no repetitiva en estado en un ciclo; si la frecuencia es 50Hz, I _t ² = 0.005 I _TSM ² (Amperios ² · seg)

Fórmulas de cálculo de generación de calor

---

Cuando los relés de estado sólido funcionan, el circuito de salida tiene una caída de voltaje de 1 ~ 2V. Cuando los módulos de estado sólido (o módulos de alimentación) funcionan, el circuito de salida tiene una caída de voltaje de 2 ~ 4V. Y la energía eléctrica que consumen se transmite como calor, y este calor solo está relacionado con su corriente de funcionamiento. El relé de estado sólido tiene un valor calorífico de 1.5 vatios por amperio (1.5 W / A) y el módulo de estado sólido tiene un valor calorífico de 3.0 vatios por amperio (3.0 W / A). El calor generado por el circuito trifásico es la suma del calor generado por cada fase.

Relé de estado sólido monofásico o de CC: P = 1.5 · I
Módulo de estado sólido monofásico o de CC: P = 3.0 · I
P es el calor generado por el relé de estado sólido / módulo de estado sólido, y la unidad es W; I es la corriente de carga real, y la unidad es A.

Normalmente, si la corriente de carga es de 10 A, se debe equipar un disipador de calor. Si la corriente de carga es de 40 A o más, se debe equipar un disipador de calor refrigerado por aire o agua.

Fórmulas de cálculo de disipación de calor

---

El rendimiento de disipación de calor del disipador de calor está relacionado con su material, forma, diferencia de temperatura, etc.

Q = h · A · η · ΔT
Q es el calor disipado por el disipador de calor; h es la conductividad térmica total del disipador de calor (W / cm ² · ° C), generalmente el material de aluminio es de aproximadamente 2.12W / cm ² · ° C, el material de cobre es de aproximadamente 3.85W / cm ² · ° C, y el material de acero es de aproximadamente 0,46 W / cm ² ° C; A es el área de superficie del disipador de calor (cm ² ); η es la eficiencia del disipador de calor, que está determinada principalmente por la forma del disipador de calor; ΔT es la diferencia entre la temperatura máxima del disipador de calor y la temperatura ambiente (° C).

Por lo tanto, se puede obtener de la fórmula anterior que cuanto mayor es el área de superficie del disipador de calor, mayor es la diferencia con la temperatura ambiente y mejor es el rendimiento de disipación de calor.

Conversión de unidad común

---

1MΩ = 10 ³ kW = 10 ⁶ Ω = 10 ⁹ mO
1F = 10 ³ mF = 10 ⁶ mF = 10 ⁹ nF = 10 ¹² pF
1H = 10 ³ mH = 10 ⁶ uH
1MV = 10 ³ kV = 10 ⁶ V = 10 ⁹ mV = 10 ¹² uH
1kA = 10 ³ A = 10 ⁶ mA = 10 ⁹ μA
1W = 10 ³ mW = 1J / s = 1V · A
1HP = 0,75 kW
1 kW · h = 10 ³ W · h = 10 ³ V · A · h = 10 ⁶ V · mA · h = 3.6 · 10 ⁶ J
1 cm = 10 mm = 0.39in
1cm ² = 0.16sq en
° F = 1.8 ° C + 32
K = ° C + 273.15

BREVE MANUAL DE SEGURIDAD

¡SEGURIDAD PRIMERO!

No hay nada más importante que proteger su propia seguridad.

Observe estrictamente las reglas de operación segura y las instrucciones de operación. Si no puede mantenerse a salvo, deje de operar y salga de inmediato. Si encuentra un problema incierto o insoluble, consulte al personal técnico pertinente a tiempo, no corra riesgos. Antes de usar, probar y mantener dispositivos eléctricos, debe saber lo siguiente:

§ 1. ¿Cuáles son los peligros de la electricidad?

La electricidad hace que nuestra vida sea más conveniente, pero al mismo tiempo también puede causar un gran daño a nuestro cuerpo vulnerable debido a su enorme energía. El daño eléctrico al cuerpo humano se puede dividir en: descarga eléctrica (como hormigueo, sensación de ardor, espasmo, parálisis, coma, fibrilación ventricular o detención, dificultad para respirar o parada respiratoria); Lesiones eléctricas (como quemaduras eléctricas, metalización de la piel). Cuando la corriente eléctrica atraviesa el corazón, puede causar disfunción cardíaca, destruyendo el ritmo de contracción y expansión original, insuficiencia cardíaca y finalizando la circulación sanguínea, causando la muerte por hipoxia en el cerebro. Cuando la corriente eléctrica pasa a través del sistema nervioso central (cerebro y médula espinal), puede causar parada de la respiración y parálisis. El efecto térmico de la corriente eléctrica puede causar quemaduras eléctricas. El efecto químico de la corriente eléctrica puede causar quemaduras eléctricas y metalización de la piel. El efecto electromagnético de la corriente eléctrica también producirá radiación. La lesión anterior puede causar daños secundarios.

Según las diferentes reacciones del cuerpo humano después de contactar la corriente, la corriente se puede dividir en los siguientes cuatro niveles:
1. Corriente percibida: el valor mínimo de corriente que puede sentir el cuerpo humano pero que no causa reacciones fisiológicas dañinas. que es 1mA (AC, 50 ~ 60Hz) o 5mA (DC) para adultos.
2. Corriente de reacción: el valor de corriente mínimo que puede hacer que los músculos se contraigan inconscientemente, que es 5 mA (CA, 50 ~ 60 Hz) o 25 mA (CC) para adultos.
3. Corriente segura: el valor de corriente máximo que el cuerpo humano puede eliminar libremente de la fuente de alimentación sin daños patológicos después de una descarga eléctrica, que es de 10 mA (CA, 50 ~ 60Hz) o 50 mA (CC) para adultos.
4. Corriente fatal: el valor de corriente mínimo que puede causar fibrilación ventricular y es potencialmente mortal, que generalmente es de 50 mA (CA, 50 ~ 60Hz), 80 mA (CC) para adultos.

La resistencia eléctrica de la piel humana es 1000 ~ 3000Ω (normalmente) y 800 ~ 1000Ω (cuando se destruye la capa externa córnea de la piel), por lo que el voltaje de seguridad se puede calcular de acuerdo con la ley de Ohm (I = U / R). Dado que la resistencia de la piel se ve afectada por muchos factores (como la ropa, el sudor, el polvo conductor en el aire), elegir el voltaje seguro es más razonable en lugar de la corriente segura. En un ambiente seco, el voltaje de seguridad es de 24 VCA (50 ~ 60 Hz) o 120 VCC; En un ambiente húmedo, el voltaje de seguridad es de 12VAC (50 ~ 60Hz) o 40VDC.

§2. ¿Cómo evitar el peligro de la electricidad?

1. Aislamiento eléctrico

El objeto cargado eléctricamente (o cuerpo cargado) debe estar encerrado por un material aislante no conductor. Mantener el aislamiento de las líneas de distribución y los equipos eléctricos es el requisito previo más básico para garantizar la seguridad personal y el funcionamiento normal de los equipos eléctricos. El rendimiento del aislamiento eléctrico se puede medir por su resistencia de aislamiento y resistencia dieléctrica.

2. Distancia de seguridad

Los objetos cargados eléctricamente deben mantenerse a cierta distancia del suelo, el cuerpo humano, otros objetos cargados y otras instalaciones o equipos. Fuera de dicha distancia de seguridad, no hay peligro cuando el cuerpo humano u objeto está cerca del cuerpo cargado, como la distancia de seguridad para el dispositivo de distribución de energía, la distancia de seguridad de mantenimiento y la distancia de seguridad de operación.

3. Capacidad de carga de corriente segura

La capacidad de transporte de corriente segura es la cantidad máxima de corriente que se permite que pase continuamente a través del dispositivo. Si la corriente excede la capacidad de transporte de corriente segura del dispositivo, el calor generado por el dispositivo excederá su valor permitido, lo que causará daños a la capa de aislamiento e incluso provocará fugas eléctricas e incendios. Por lo tanto, antes de seleccionar un dispositivo, debe conocer su capacidad de carga de corriente segura.

4. Marcado

El marcado claro, preciso y uniforme es otro requisito previo importante para garantizar la seguridad de la electricidad. Por ejemplo, la zona peligrosa debe marcarse con una marca de advertencia, el dispositivo con una estructura diferente y diferentes parámetros pueden identificarse con la marca del número de modelo, los cables con diferente naturaleza y diferentes propósitos pueden identificarse mediante una marca de color (por ejemplo, Fase Un cable es amarillo, el cable de Fase B es verde, el cable de Fase C es rojo, el cable a tierra expuesto es negro; el circuito de CA del circuito secundario del sistema es amarillo, la fuente de alimentación negativa es azul y la señal y los circuitos de advertencia son blancos).

§3. Cómo operar de manera segura

1. Equipo de protección

Antes de operar el dispositivo eléctrico, asegúrese de haber usado guantes con aislamiento de goma, zapatos con aislamiento, ropa antiestática, gafas de seguridad y otro equipo de protección. Y también debe confirmar que hay instalaciones para combatir incendios u otras instalaciones de seguridad dentro del rango especificado.

2. Herramientas de operación

Debe verificar si la herramienta que está utilizando tiene capacidad de aislamiento, si el material de aislamiento está envejecido y se ha caído, debe reemplazarse de inmediato. Si existe riesgo de explosión e incendio, use una herramienta a prueba de explosión.

3. Precauciones de operación

● No opere con energía.
● Asegúrese de que el entorno de trabajo esté seco, que la temperatura sea adecuada y que las condiciones de ventilación sean buenas.
● Asegúrese de que la mesa de trabajo esté limpia y libre de polvo, desechos metálicos, etc.
● Asegúrese de que los cables estén conectados correctamente de acuerdo con la marca. Para dispositivos de CC, no invierta los polos positivo y negativo.
● Asegúrese de que todos los equipos eléctricos y electrónicos funcionen dentro de su valor nominal.
● Asegúrese de que todo el dispositivo esté conectado a tierra de forma segura.
● Si hay una gran capacitancia o una gran inductancia en el dispositivo, no puede tocarlo directamente incluso después de que se apaga la alimentación, ya que generará un alto voltaje de varios miles de voltios en un instante. Debe esperar su descarga natural o forzar la descarga utilizando equipos auxiliares en condiciones seguras.
● Antes de usar el dispositivo de regulación de voltaje, asegúrese de que el regulador esté en el estado inicial (voltaje cero, 0V).
● Cuando utilice equipos eléctricos o electrónicos, una vez que huela el olor a quemado, escuche sonidos anormales, vea condiciones anormales como el parpadeo de la pantalla o la luz indicadora, apague inmediatamente la alimentación y verifique el equipo.
● Si el dispositivo necesita ser reemplazado debido a un mal funcionamiento, se recomienda utilizar un dispositivo con el mismo modelo o parámetros técnicos.
● No presione el botón de parada inmediatamente después de arrancar el motor eléctrico, ya que su corriente de arranque es de 6 a 7 veces la corriente nominal, si se detiene inmediatamente, quemará otros equipos.